The energy of a photon with frequency
 is is 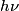 , where , where 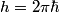 is Planck's constant. Assuming all of this energy is transferred to a single a electron, the electron will have energy is Planck's constant. Assuming all of this energy is transferred to a single a electron, the electron will have energy 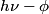 after being ejected from the metal. The potential difference required to decelerate such an electron until it stops is after being ejected from the metal. The potential difference required to decelerate such an electron until it stops is 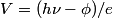 . So, the slope of the line is . So, the slope of the line is 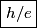 . Therefore, answer (B) is correct. . Therefore, answer (B) is correct. |